Tidetech's models are based on the 2-dimensional depth-integrated tide-surge model developed by the Proudman Oceanographic Laboratory, UK over many years. These models have been used to provide the UK Storm Surge Forecasting Service operated by the UK Met Office including determining closure of the Thames Barrier and have been used in many research projects related to storm surge inundation, tidal power, larval and oilspill fate studies, palaeotidal studies and climate change scenarios to name a few.
They solve the classic shallow-water equations for momentum and continuity to produce depth-averaged currents and sea surface heights relative to mean sea level. The model is formulated in structured finite differences with 2nd order accuracy on an Arakawa C grid – this assumes sea surface height and bathymetry are located at the centre of a cell and velocities described at the centres of the cell sides as in the diagram below.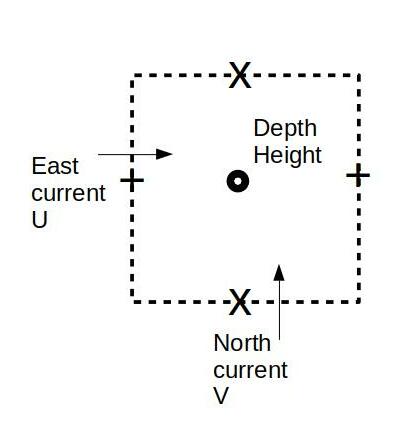
Fig 1. Arakawa C-grid
Normally the model is applied to a region, although it can be applied globally. When applied regionally it is typically in a nested configuration with local areas resolved down to the scale of 100m where suitable bathymetry is available. In a typical set up the following information is required to compute the tidal response:
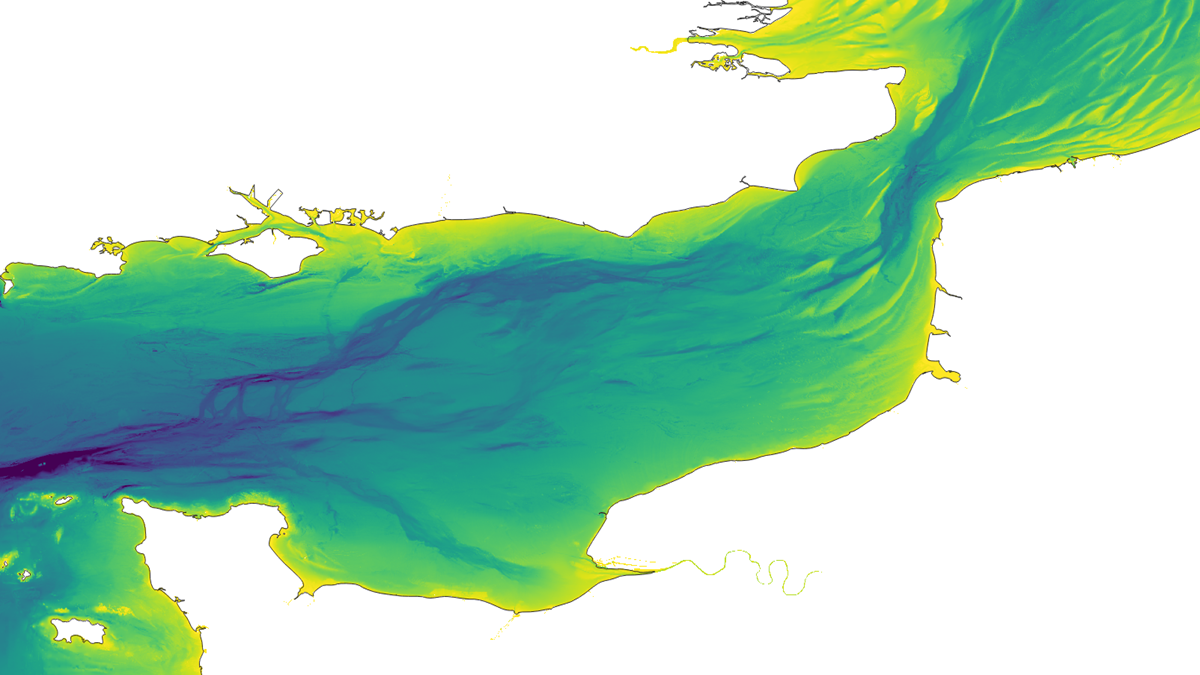
Fig 2: English Channel High Resolution (100m) Bathymetric Data
If tide and storm surge interaction are needed the model also requires:
Typically the meteorological and open boundary forcings come from larger domain models, and are interpolated to the required model domain and resolution, although it is possible to utilise observations where available.
These models integrate the tidal (and storm surge) response through time. Usually starting from a rest state (i.e. heights and currents set to zero), or from a pre-defined state, the open boundary input (and surface meteorological forcing, but note below) is updated every model timestep and adjacent model cells respond to this, changing the currents and heights ensuring conservation of volume. The model cells next to these then respond in a similar manner. In this way the open boundary forcing is propagated throughout the model domain. After a suitable period of time, usually a few days, each model cell achieves an equilibrium with its neighbours and the model is considered in dynamical balance. Usually, the surface meteorological forcing is applied once this balance is achieved so as to avoid the potential for instabilities to be introduced by sudden shock forcing.
The example below shows the application of the tidal model to the region of Singapore Straits. The open boundary of the model is set sufficiently far from the regions of interest (Malacca and Singapore Straits) so there is certainty that dynamical balance has been achieved.
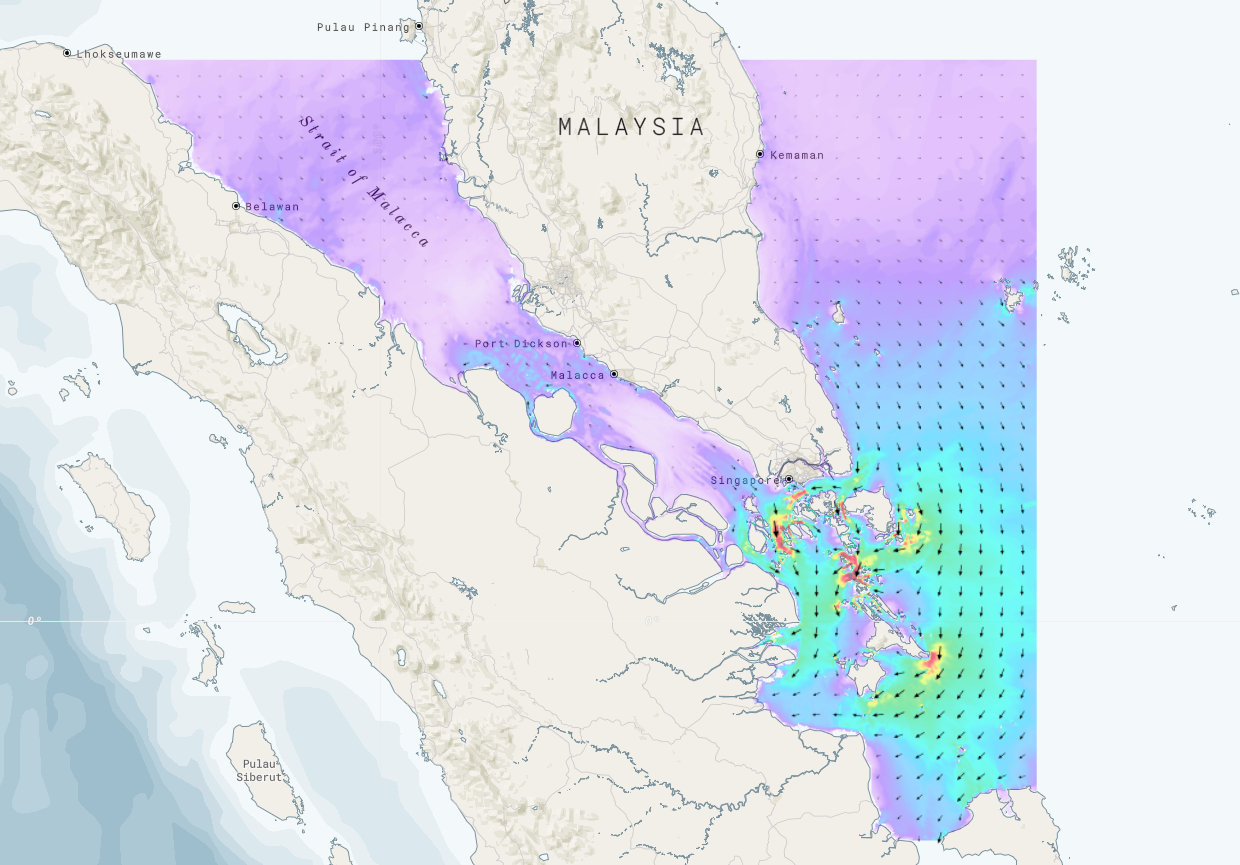
Fig 3. Malacca and Singapore Straits Tidal model
Tidal heights and currents are computed at each node, approximately 900m apart, and each node responds to the nodes around it. The figure below shows a snap shot in time close to maximum flood tide, with currents (in red) of 2 knots.
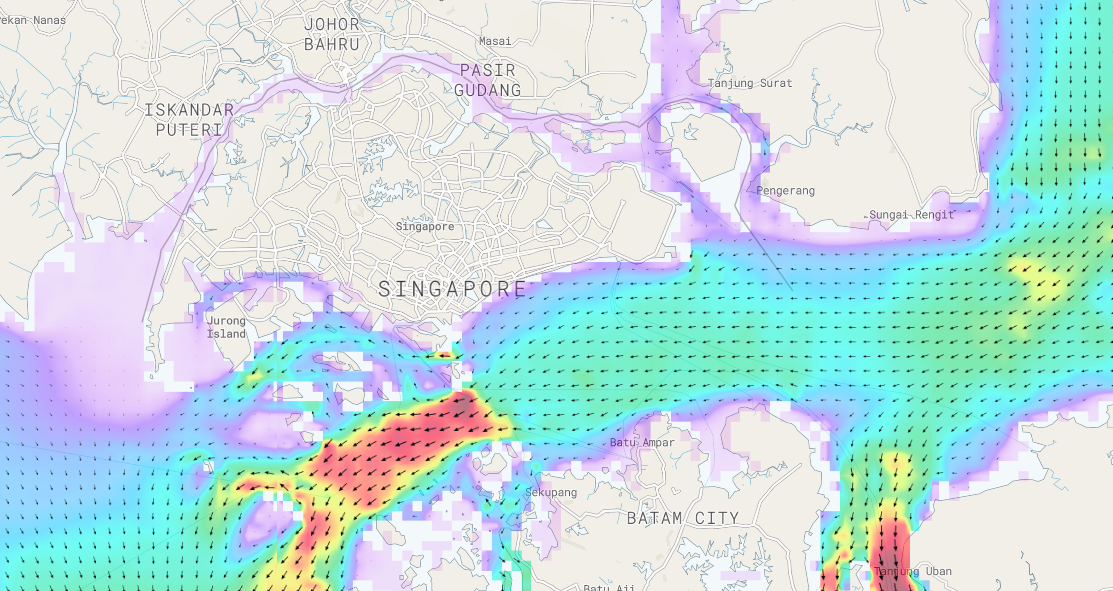
Fig 4. Singapore Straits tidal currents
Because of the nature of tides, i.e. a response to gravitational attraction of the Moon and Sun, they can be computed for any time in the past or the future, provided that no significant changes to bathymetry or coastlines have been made to impact on the dynamic equilibrium. If significant changes happen, e.g. due to major dredging or new island formation, then new bathymetry and coastline need to be sourced and the response to these changes recomputed.
